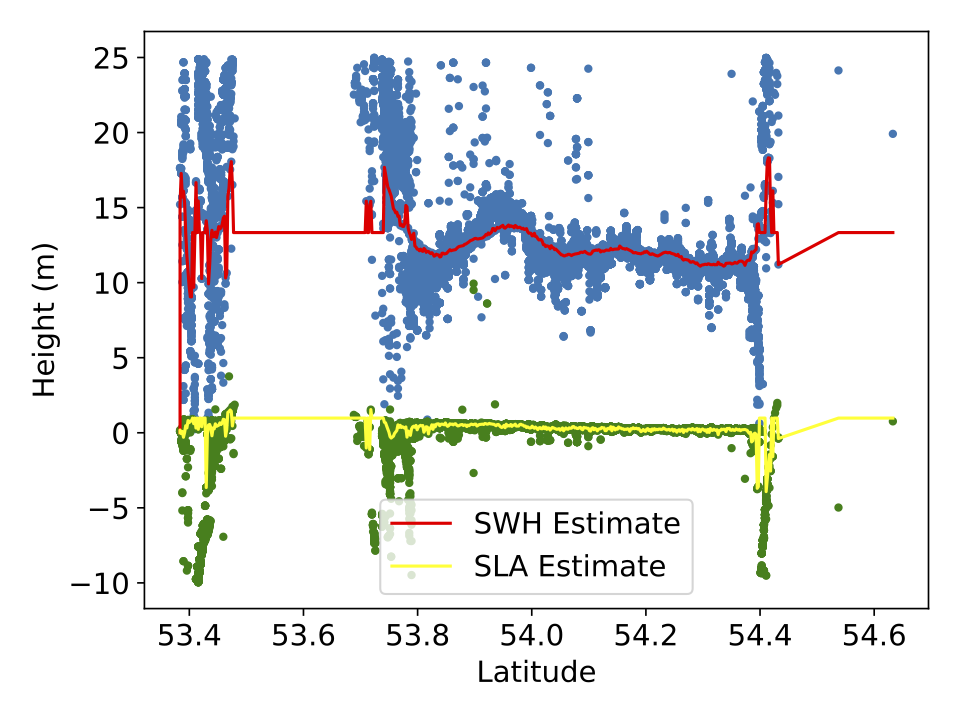
In geodesy, multi-objective optimization problems are ubiquitous. An example from project C1 are clustering and aggregation problems in cartography where one has to cluster areas and aggregate them into larger regions and there are multiple objectives one wants to optimize. Another example from project C2 comes from satellite radar altimetry of the sea surface where one wants to estimate both the sea surface height (SSH) and the significant wave height (SWH) from satellite data, which leads to a multi-objective shortest path problem.

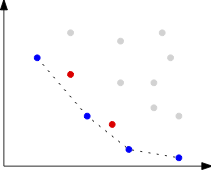
A common approach to handle multi-objective optimization problems is to combine the different criteria into a single objective by taking a weighted sum. This weighting is often artificial and can result in a loss of information. We will make use of the full potential of multi-objective optimization and study in particular the set of Pareto-optimal solutions.

We will develop algorithms for efficiently computing or approximating this set for the problems mentioned above and other problems motivated by applications from geodesy. We will collaborate with A2, B1, B2, and C1 on multi-objective clustering and aggregation problems, with C1 and C2 on multi-objective triangulations, and with B2, C1, and C2 on multi-objective shortest path problems. Our algorithms will be analyzed theoretically but also implemented and tested in cooperation with projects C1 and C2 as well as B2. This will lead to both improved solutions in practice and novel theoretical results.

Results include the first output-sensitive algorithm for the complete Pareto set of bicriteria polygon aggregation (ESA 2025), the first systematic study of approximately Pareto-optimal bi-objective clusterings (NeurIPS 2024, with A2), and a classification of the approximability of connected clustering for several central objectives and graph classes (Algorithmica 2024 and ESA 2025, with A2; ESA 2026). Further results concern the price of hierarchical clustering (Algorithmica 2025), minimum tree covers in all symmetric monotone norms (STACS 2025), doubly constrained fair clustering (SWAT 2026, with A2), the DBA algorithm for averaging time series (Data Mining and Knowledge Discovery 2025, with B1), and regions of maximum circularity (arXiv 2026, with C1). Joint work on map aggregation and interactive maps appeared in ACM TSAS 2025 (with B1 and C1) and IEEE TVCG 2025 (with B1, B2 and C1). See our publications.

This project focuses on the aspect of side constraints in the context of clustering, aggregation and simplification problems from geodesy and on the question to what extent it is possible to efficiently find approximative solutions for constrained problems. Side constraints occur naturally both in the process of digitally designing maps and in sea surface representation.

Clustering problems as studied in combinatorial optimization are often NP-hard even without side constraints, i.e., it is most likely not possible to solve them optimally in polynomial time. Typical solutions for this are to use ILP formulations and speed up (exponential-time) algorithms in practice, or to design application specific heuristics. An alternative are approximation algorithms: These aim to find solutions with a provable worst-case guarantee in polynomial time. For classical clustering algorithms, there exists a large variety of approximation algorithms.

Although clustering problems arising in geodesy are often related to those clustering problems that are studied extensively in the theory and algorithms community, they differ in important aspects: a) They involve many side constraints and b) the input objects can be complex objects like polygons, graphs or time series. In this project, we aim to advance the state-of-the-art for approximation problems for clustering of complex geometric objects under side constraints.

Motivated by a question from C2, the project developed together with A1 the theory of connected clustering, in which every cluster must form a connected part of a given proximity graph such as the coastline (Algorithmica 2024 and ESA 2025, with A1). Applied to tide-gauge stations, the resulting groups of stations reconstruct global mean sea level more accurately than using all stations. Further results include approximately Pareto-optimal bi-objective clusterings (NeurIPS 2024, with A1), constant-factor approximations for doubly constrained fair clustering (SWAT 2026, with A1), and connected subspace clustering of satellite-altimetry data (arXiv 2026, with A1, A3 and C2). See our publications.

Due to vast amounts of sea surface height data and very large geographical data sets, there is an increasing need for highly scalable clustering methods that deal with geometric data representations. Therefore, main objective of this project within the RU is to develop and analyze new algorithmic concepts to improve scalability of geometric clustering algorithms with provable guarantees.

In order to achieve this goal, we will develop new concepts of dimension reduction for geometrically represented objects such as polygonal curves and corresponding distance measures such as the Fréchet distance. For center-based clustering methods with complex geometric centers such as subspace clustering, we will develop new sampling approaches to reduce the number of input points and for clustering of geometric objects we will develop new data reduction methods that combine simplification, dimension reduction and sampling methods to improve scalability of algorithms.

We will implement and engineer the most promising approaches and provide them as new tools to projects C1 and C2 to study problems in the context of map aggregation and sea level height analysis, representation and reconstruction.

Results include the first approximation schemes for (k,ℓ)-clustering of curves under the Fréchet distance whose running time is polynomial in k (ICALP 2026, with B1) and a new time-series decomposition based on the Fréchet distance (ESA 2026, with B1), which led to a DTW-based alternative to PCA in sea-level geodesy (EGU 2024, with B1 and C2). Further results include dimension reduction for curves (ESA 2026), sublinear algorithms for estimating single-linkage clustering costs (ESA 2026), average sensitivity of geometric algorithms (ITCS 2026), a subquadratic algorithm for individually fair k-center (AISTATS 2025), and a scalable approach to connected subspace clustering of satellite-altimetry data (arXiv 2026, with A1, A2 and C2). See our publications.

Algorithms in geodesy often need to determine if two geometric objects are similar or dissimilar. Depending on the specific application, the algorithm needs to be provided with a definition of this dissimilarity, which is usually done in the form of a mathematical distance measure. Broadly speaking, the aim of this bridge project is to study the mathematical structure and complexity of several distance measures relevant to this RU on two levels: (i) on the level of the distance between two individual objects via a study of the complexity of the distance computation, and (ii) on the level of the entire metric space via a study of the VC dimension of the corresponding set system of metric balls.

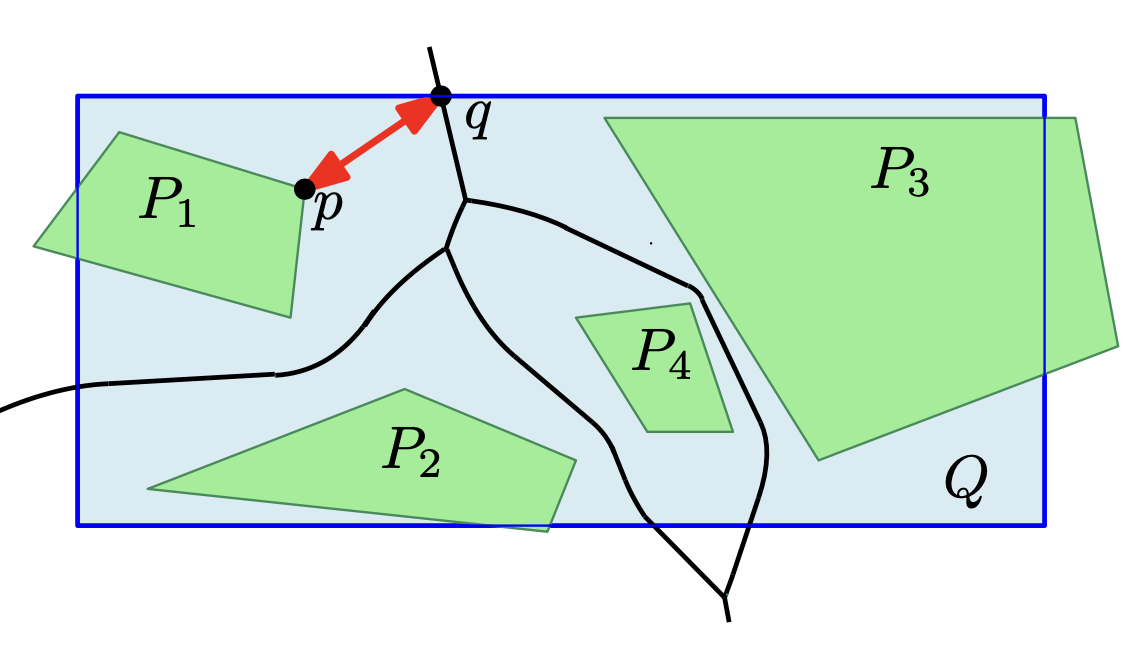
We will explore adaptations of different geometric distance measures, such as the Fréchet distance and the Hausdorff distance, which are known to capture continuous geometries well. The distance measures are developed in close collaboration with the geodesy experts of projects C1 and C2 and algorithms experts of A1, A2, A3, and B2 to ensure (i) suitability to the application and (ii) efficient computability. In this way, the project is closely integrated into collaborations across the entire RU.

The ultimate goal of the project is to study new algorithmic methods for clustering, aggregation and simplification involving polygonal curves and polygonal regions. The new methods should be applicable to cartographic generalization, as well as clustering of ocean remote sensing data. In both cases, the algorithm should find a compact representation of geometric objects which maximizes the similarity to the measured data points under an appropriate definition of geometric similarity. To achieve the goal of wide applicability, we study the clustering and aggregation problems that arise within this RU within the framework of geometric set cover formulations.

The project obtained faster algorithms for the Fréchet distance of time series (ESA 2024, SoCG 2025), culminating in the Best Student Paper Award at SoCG 2026. Further results include property testing of curve similarity (ESA 2025), the fine-grained complexity of continuous Euclidean k-center (STOC 2026), the expiration streaming model (ICALP 2026, with B2), subtrajectory clustering (ESA 2025), applied to ocean drifters together with C2, approximation schemes for clustering curves and a Fréchet-based time-series decomposition (ICALP 2026 and ESA 2026, with A3), the DBA algorithm (Data Mining and Knowledge Discovery 2025, with A1), and polygon aggregation with arbitrary shapes (ESA 2026, with B2 and C1). See our publications.

Within our RU graphs appear directly as cartographic maps or indirectly as their geometric dual graphs, as shortcut graphs or as triangulations. Within this project, we will consider these structures as geometric graphs, i.e. graphs embedded on the plane (or on a surface). These graphs are often sparse, even planar, and thus allow for more efficient graph algorithms than general graphs.

We will develop algorithmic engineering approaches for practically solving discrete optimization problems on geometric graphs related to the clustering, aggregation, and simplification problems that occur within our RU. An important goal is to speed up and to improve the quality of combinatorial as well as integer-linear-programming approaches for discrete (multi-objective) optimization problems on geometric graphs. This will be achieved by carefully taking the graph topology and the (geometric) structure of the given input data into account, sometimes in combination with learning approaches. For some of these problems, new similarity measures for geometric graphs, which we will develop jointly with B1, will play an important role. Another important ingredient are carefully engineered data structures to support queries about graphs and interactive maps.

As a bridge project, jointly with B1, we will make sure that the theoretical concepts and algorithms suggested in projects A1, A2, and A3 will find a suitable realization in the geodesy projects C1 and C2. Our work program is closely interlinked with all the other subprojects.

Highlights include strong ILP formulations that solve the p-regions problem for entire European countries (ESA 2026, with C1), new ILP models for the graph edit distance (VLDB 2025), graph-similarity measures for building footprints (ACM SIGSPATIAL UrbanAI 2023 and ACM SIGSPATIAL 2026, with C1), a simpler and practically efficient parametric minimum-cut algorithm for hierarchical polygon aggregation (ALENEX 2025), polygon aggregation with arbitrary shapes (ESA 2026, with B1 and C1) and over time (ACM SIGSPATIAL 2026, with C1), optimality-preserving data reduction for maximum k-cut (ESA 2026), and a Weisfeiler–Leman approach to message passing in temporal graphs (NeurIPS 2026). See our publications.

To use a geographic data set in a spatial analysis or for a map, one often needs to coarsen its granularity. In geographic information science and cartography, this task is termed generalization. Project C1 will contribute to automated generalization by developing algorithms for detecting groups of objects in a geographic data set and computing a single representative and simplified object for each group.

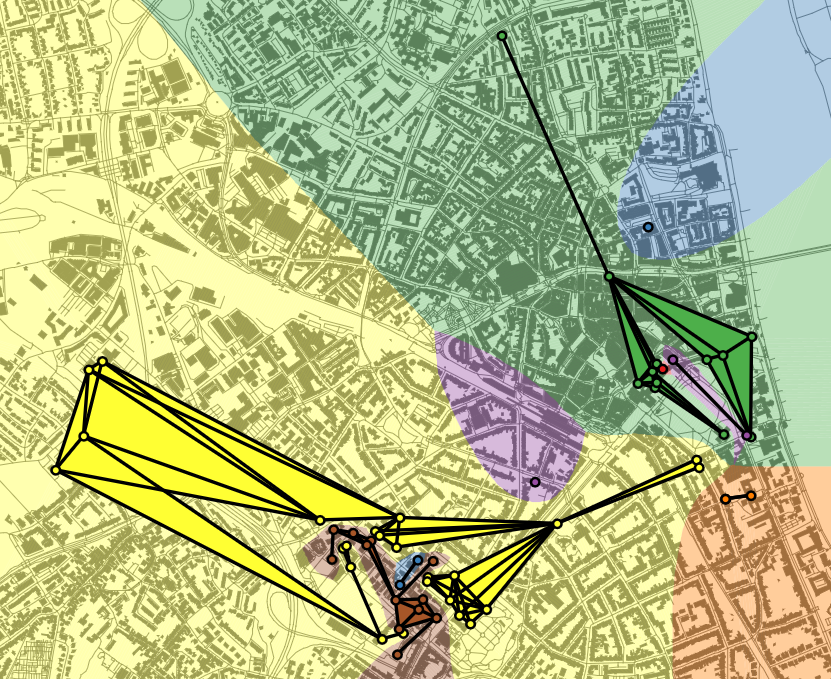
As two concrete use cases we will study (i) the delineation of regions of human activity based on geo-tagged social-media data and (ii) the derivation of polygons corresponding to built-up areas, settlements, and larger urban agglomerations from footprints of individual buildings. In both cases we aim at interactive maps that allow their users to zoom through different scales and to change the map's point of reference in time or its interval of reference in time. For example, by dragging a time slider, a user can change the map's point of reference in time to obtain an animation of urban growth over multiple years.

We will develop an approach that treats the detection of groups of objects, the aggregation of each group to a polygon, and the simplification of polygons as a single task. Our central hypothesis is that such an integrated approach yields substantially better solutions than the currently dominating approach of first aggregating and then simplifying. The development will follow an algorithm engineering process including the modelling of problems, the design of efficient algorithms, mathematical analyses, and experiments.

Results include an optimization-based aggregation of building footprints into settlement areas (ACM TSAS 2025, with A1 and B1; ISPRS Annals 2026, with B2; ESA 2026, with B1 and B2), scalable many-to-many matching of building polygons across datasets (ESA 2024, Information Fusion 2025, International Journal of Digital Earth 2026), graph-based similarity measures for building footprints (ACM SIGSPATIAL UrbanAI 2023 and ACM SIGSPATIAL 2026, with B2), strong ILP formulations for regionalization (ESA 2026, with B2), simultaneous selection and displacement of buildings and roads (IJGIS 2025), and algorithms for consistent interactive maps with a time-slider interface (IEEE TVCG 2025, with A1, B1 and B2). See our publications.

Project C2 will address questions that are fundamental to our understanding of climate change: What are the regional rates of sea level rise? How is regional sea level rise related to changes in sea level extremes and to changes in sea state? To what extent do satellite observations of the sea surface fit to modelling of ocean heat change (OHC)? Which patterns of heat redistribution can be derived from satellite observations?

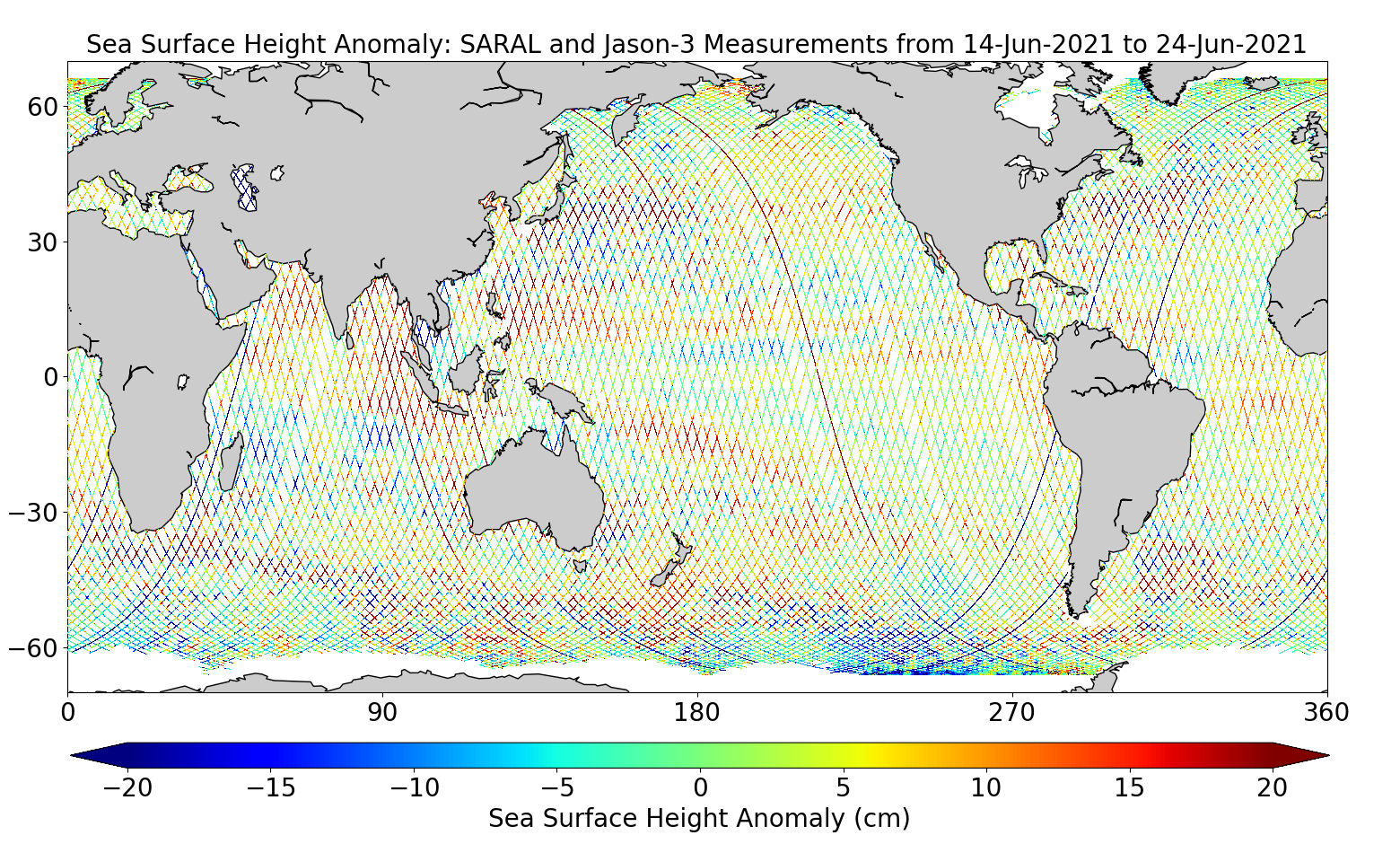
We will explore the synergy in the RU to better exploit the vast archive of satellite data and ocean modelling. New and efficient methods for geometric representation and clustering data will be tailored to the problem (AI methods have been introduced in ocean remote sensing before, but these were mostly transferred from image analysis and often did not properly account for the geometrical nature of the problems).

Thus, within this RU, we decided to address four particular problems with novel AI-based methods: (1) Consistent analysis of radar echoes for sea surface height (SSH) and significant wave height (SWH), (2) Combining and analysing SSH variability, (3) Reconstructing multi-decadal SSH with sparse data, and (4) inverting radar observations of SSH into OHC. These problems follow the analysis chain in sea level research, but they can be addressed independently.

Connected clustering of the altimetry grid (arXiv 2026, with A1, A2 and A3) and a DTW-based alternative to PCA/EOF (EGU 2024, with A3 and B1) reveal ocean regions with clear geophysical meaning, such as signals of El Niño–Southern Oscillation (ENSO). These representations feed into the joint inversion of satellite altimetry, GRACE gravimetry and Argo profiles for ocean heat content (Earth System Science Data 2026, see the press release of the University of Bonn) and into consistent estimates of the sea-level budget (Journal of Geodesy 2022, Geophysical Journal International 2026). Minimum-error triangulations for reconstructing the sea surface from tide gauges were developed jointly with A1, B1, B2 and C1 (Journal of Computational Geometry 2023). See our publications.